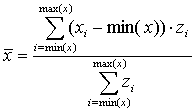 |
(1) |
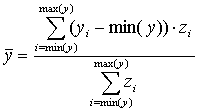 |
(2) |
高度平衡多邊形法之數值計算
Numerical Algorithm of Height Balance Polygons Method
| *鄭子璉 | ** 周乃昉 | ***胡文盛 |
| Tze-Lien Tseng | Frederick N. Chou | Wen-Hseng Hu |
摘要
估算集水區平均降雨量常採用算數平均法、徐昇多邊形法與等雨量線法進行分析,惟高度平衡多邊形法以雨量站高程校正所分配之權值,一般認為此法於地形崎嶇地區較徐昇多邊形法為佳,但因計算過程繁雜,以致分析不易,其應用亦相對減少。
本研究發展電子計算機高度平衡多邊形法的數值計算模式,支援中央大學太空遙測中心之數值高程資料檔及 ArcView 圖檔,可迅速依序求得雨量站之三角網、高程中點三角網及高度平衡多邊形網,並利用自行發展交集分析模式,求出各雨量測站在集水區內的控制面積加權因子,有助於現場即時估計平均降雨量。
關鍵字:高度平衡多邊形、三角網、平均雨量、集水區
Abstract
Arithmetical averaging method, thiessen polygons method and isohyetal method are used for estimating the areal rainfall of watershed. The height balance polygons method (HBPM) is considered to be prior when being applied in the roughed surface of watershed, for that the weighted function is calculated according to the elevations of rainfall gauges. However, due to the complexity of calculation, the HBPM is difficult in routine operation.
A numerical algorithm, which supports the DTM and ArcView files is developed in present study. The triangulated irregular networks (TIN), center point of elevation of TIN, height balance polygons can be gained. With the self-developed intersection Analysis model to be computed the weighted factors of real-time average rainfall could be estimated automatically and efficiently.
Key word: height balance polygons, triangulated irregular networks, areal rainfall, watershed
一、前言
1.1 研究背景
在集水區中由點降雨推估全流域之平均降雨有很多方法,一般常用之方法有算數平均法、徐昇多邊形法與等雨量線法等,在此多種分析方法外,另有高度平衡多邊形法 (Height Balance Polygons Method) 考慮集水區地形高程變化,藉此推估各點雨量對集水區平均降雨量之影響,但因計算過程繁雜,較少利用此法分析區域平均降雨。
近年來由於地理資訊系統快速發展,高度平衡多邊形法所需之地理基本資料建構漸趨完整,除可利用衛星定位系統快速取得雨量站座標,並可結合中央大學太空遙測中心所提供的數值高程資料 (DTM) 檔取得集水區內各座標的高程資料,以此基本資料較易建立計算機數值分析模式。
1.2 研究目的
以高度平衡多邊形法求出之平均降雨量精確度較算術平均法為佳,但由於高度平衡多邊形網若以人工方式繪製,須耗費相當的時間及人力,且其中若有一雨量站移動、增設或裁撤,則整個高度平衡多邊形網便須重新繪製,若應用於即時防洪預警系統中,可能因電傳雨量站故障導致必須重新計算分析,若以人工作業進行本項分析,將無法配合即時防洪預警系統的時效。
因此在研究中利用電子計算機建立完整高度平衡多邊形法數值分析模式,可迅速完成高度平衡多邊形網的繪製與計算,並計算出每一個雨量測站的高度平衡加權因子,有助於現場估計即時平均降雨量的計算應用。研究中以 Visual Basic 為發展工具,並直接取用中央大學太空遙測中心之數值高程資料檔,在分析上包含雨量站三角網分析、三角網連線上兩雨量站高程中點分析、高程中點三角網分析、高度平衡多邊形網、交集分析與高度平衡加權因子計算。
二、研究基礎
高度平衡多邊形法為區域平均雨量估計的計算方法之一,特別在暴雨或颱風期間平均雨量的估計正確與否,往往影響水庫操作及下游水位的估算,相關平均雨量估計方法經常被提出檢討。
由王如意等人[1]的研究得知,高度平衡多邊形法多用於地勢崎嶇、山嶺險阻之區域,各雨量站除經過加權分配,且加以高程之修正。其法為先標明各水文站之標高,然後連接相鄰兩站,取其標高之中點處,該標高之中點處不一定為該兩站連接線之中點。再連接各標高中點成甚多個三角形,再做各三角形之內角等分線,交於各三角形之內心。連接各內心可圍住一雨量站,此面積即為該雨量站之標高及所控制之面積,適合地形崎嶇多變之地區,惟其應用手續繁瑣費時。
在高度平衡多邊形法中以高程加權雨量站所分配之控制權重,一般認為徐昇多邊形法僅考慮二維平面權值分配,若在地形崎嶇多變之地區,應用高度平衡多邊形法會較徐昇多邊形法為佳。
三、分析方法
由前述說明中得知研究中,在進行高度平衡多邊形法計算應先進行雨量站三角網 (TIN) 分析,其後根據三角網中各三角形連線上兩兩雨量站進行高程中點分析,並得到高程中點三角網,以相鄰高程中點三角網各三角形內心兩兩相連可得到高度平衡多邊形網、以高度平衡多邊形網與流域多邊形交集分析炳計算與流域多邊形面積的比值得到與高度平衡加權因子。
(一)雨量站三角網分析
三角形的形狀影響高度平衡多邊形法估算加權因子的正確性及精確度,由不同組的三個雨量站所形成的三角網,以每個三角形都接近正三角形最為理想,但雨量站之分佈位置受地形及故障等情況影響,實難以達此理想。因此本研究中三角網之決定,以採用任三個雨量站所決定的外接圓內不含其它雨量站者構成一個三角形,利用此法可決定出較為理想的三角網。
(二)平均高程中點位置分析
高度平衡多邊形法在計算分析上的核心即為高程中點的決定,在本研究中以兩雨量站間平均高程中點為高程中點,從中央大學太空遙測中心所提供的數值高程資料檔中直接擷取高程資料,由高於低高程的雨量站至低於高高程的雨量站間的剖面資料進行高程加權中點之分析。高程加權中點之計算式如方程式 (1) , (2) 。
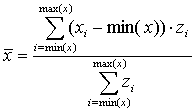 |
(1) |
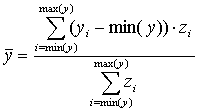 |
(2) |
其中,
| = 高程中點座標 | |
| = 兩雨量站連線的高程座標 |
在求取高程中點時,先以雨量站座標位置所處的最小格網對雨量站進行高程檢定,以降低可能因文獻紀錄資料精度不足所造成的誤差,另外在兩雨量站連線的高程擷取上,只內插求取與 DTM 圖檔格網線上的交點座標,以降低內插所可能造成的誤差累積。
(三)高程中點三角網
由已分析完成的高程中點可對應至雨量站連線之三角網上,以三角網上的高程中點所形成新的三角網即為高程中點三角網。
(四)高度平衡多邊形網
由高程中點三角網內每一頂點作對角平分線可交於各高程中點三角形之內心,並反向延伸各對角平分線至計算邊界,則可形成包含於對應雨量站的閉合多邊形,此即為高度平衡多邊形,所有對應於各雨量站的高度平衡多邊形總稱高度平衡多邊形網。
(五)多邊形交集與高度平衡加權因子
各高度平衡多邊形依序與流域多邊形進行交集分析[2],可得各雨量站在該流域中控制的閉合多邊形,計算此一多邊形與整體多邊形的比例面積即為該雨量站的高度平衡加權因子。其中交集分析採自行發展的交集演算法,以提高執行效率及計算精度。
四、應用實例
本研究採曾文水庫集水區為計算案例[3]。曾文水庫集水區集水面積為 481 平方公里,集水區內外目前共有九個電傳雨量站,在即時防洪運轉過程中,由各電傳雨量站整點傳回之雨量資料可估計集水區內的平均降雨,並可推估未來數個時段內水庫可能的進水量,以此資料可進行水庫的防洪運轉操作。若在即時防洪運轉過程中發生電傳雨量站故障,應立即依可正常作業中之電傳雨量站重新分析各雨量站的高度平衡加權因子,以利推估平均降雨,若能應用電子計算機進行分析,將可大幅提高分析效率。
為求精確計算各雨量站所控制之面積,在研究中利用全球定位系統 (GPS) 至現地各雨量站進行座標校正,並以校正後之雨量站座標進行分析,如表 1。
五、結果與討論
5.1 分析結果
圖 1 為已分析完成的螢幕展示畫面,圖面展示了分析完成之三角網、高程中點三角網、高度平衡多邊形網及與集水區邊界多邊形交集完成的控制區域,以 Pentium II 300 計算此案例約共需 10 秒 (雨量站 9 站,邊界多邊形 688 點) ,三角網高程中點三角網及高度平衡多邊形網分析部分約佔 2 秒,高度平衡多邊形網與流域多邊形交集約需 8 秒,圖 2 為高度平衡加權因子輸出表之螢幕展示畫面,圖 2 表格中高度平衡網交集面積欄之單位為平方公尺。
就模式計算之時效性來說,純就人工圖紙作業,約需三到七個工作天,若以本模式計算與操作,包含流域多邊形及雨量站位置數化與模式分析計算,整體作業可在 15 分鍾內操作完成。所運用的編譯器為 Visual Basic 5.0 中文專業版,分析模組可在一般慣用之 32 位元之視窗環境系統上執行 (Win32) 。
5.2 研究討論
茲就本研究進行時所遭遇困難部分提出討論。
(一)高程中點分析
高程中點在原文獻定義上是取兩點間高程恰為兩點高程平均值之點,惟電傳雨量站因考量到無線電波傳送,一般均設置於地形稜線上,因此若以此定義之高程中點分割,將使高度平衡加權因子分配十分不平均。例如圖 3 ,在表湖與三角南山連線的剖面上,兩點高程平均點與整個剖面長度的比例約為 0.5 % ,若以此定義進行高度平衡多邊形網計算,在研究中認為並不合適。且高程中點若以兩點高程平均值之點為中點,則亦有可能出現三個點以上反而造成應用上的困擾,如圖 4 ,在大棟山與樂野連線的剖面上,兩點高程平均點共計 11 個點,在高程中點反而難以選取。
(二)分析範圍邊界
靠近圖面邊緣的雨量站之高度平衡多邊形多無法閉合,而對角平分線反向將無限延長至無窮遠,因此不但不能計算高度平衡多邊形面積,也無法執行交集分析。為解決此種情況,本研究依據人工圖紙作業以有限圖紙分析高度平衡多邊形網之方式,由雨量站位置座標點與集水區邊界之資料點中找出最小及最大的 x 值與 y 值,並向圖面外延伸各軸邊長的 5 % 做為分析範圍邊界的頂點,憑以繪一矩形視為圖紙邊緣並當做分析範圍邊界。再針對各高度平衡多邊形逐一檢查其是否閉合,非閉合的高度平衡多邊形則由多重折線的起點與終點處向外延伸至分析範圍邊界,依正方向(逆時針方向)繪成一閉合多邊形;若原為閉合的高度平衡多邊形則與分析範圍邊界進行交集分析,以交集完成之高度平衡多邊形取代超過分析範圍邊界的高度平衡多邊形。附帶的,加入分析範圍邊界亦可使輸出之圖形較美觀,可依圖面內容完全展示在螢幕或圖紙上。
(三)修正高度平衡多邊形
前述高度平衡多邊形雖與分析範圍邊界進行交集分析,但實際運用分析時,有可能因雨量站座標位置發生高度平衡多邊形內自相交的情形,如圖 5 ,而此高度平衡多邊形相鄰兩多邊形亦必發生重疊,過去參考文獻中無討論到此情形之處理方式,在本研究中令從相交點作一對角平分線延伸至分析範圍邊界,憑此線段修正此三個多邊形。
若雨量站網由單一雨量站構成,則無三角網、高程中點三角網及高度平衡多邊形網,高度平衡加權因子為 1 ,若雨量站網由兩雨量站構成,則三角網為單一直線,無高程中點三角網,高度平衡多邊形網由與兩雨量站連線垂直並通過高程中點之直線與分析範圍邊界構成。
(四)匯入與匯出至 ArcView
在現有運用地理資訊系統分析中,常會因圖檔格式眾多,且不同軟體彼此之間圖檔格式互不相容,而造成應用上的困擾,因此本研究中所發展的分析模式除可使用自行定義的 ASCII 純文字格式,亦支援 ArcView 的 Shape File 格式[4],數值計算模式可由 ArcView 的圖檔匯入,如圖 6,計算完成之圖形可匯出為 ArcView 的圖檔,供其他分析使用,如圖 7。
(五)與徐昇多邊形法比較
徐昇多邊形法僅考慮二維平面的控制面積,在做圖處理亦以徐昇多邊形法較為單純,且目前此法已有多套的的現成計算機模組,因此徐昇多邊形法較常被採用於面積雨量的推算,在本研究中亦比較徐昇多邊形法與高度平衡多邊形法的分析成果,對於 9 站電傳雨量站均選取分析的狀況來說,徐昇多邊形法計算結果如圖 8,其徐昇加權因子如表 2,由於計算方法不同,徐昇加權因子與高度平衡加權因子或有增減,大體上分析結果趨近一致,對於接近線性分布的雨量站網如樂野、龍美及大棟山所構成之雨量站網來說,高程在樂野與大棟山之間的龍美高度平衡加權因子僅為其他兩站的 1/4 ,高度平衡多邊形成 T 形分布,如圖 9,但在徐昇加權因子尚維持均勻分配,徐昇多邊形成平行分布。
由此得知,高度平衡多邊形法受雨量站網分布位置影響頗大,在運用此法分析流域平均降雨量時應盡量納入所有可分析之雨量站進行分析,以提高平均降雨量計算之精度。
(六)數化誤差與計算誤差
一般流域邊界多邊形在數化或是直接利用 DTM 圖檔所得到的數化誤差,可能造成 0.5 % 以下的數化誤差,在研究中認為此誤差應較利用求積儀所描繪之面積誤差為小,並不影響高度平衡加權因子之計算,另在本研究中並修正前研究之交集分析方法,有效利用計算機變數可用的位數,使計算誤差均小於相對精度 10-14 ,使計算結果更為可靠。相較利用 ArcView 進行交集分析,可能受 ArcView 格網分析使得各計算區多邊形邊界形成階梯狀邊界,而使計算誤差大於相對精度 10-4 ,在本研究中所運用的交集分析較 ArcView 可靠,並可維持原數化精度。
六、結論與建議
6.1 結論
6.2 建議
謝誌
在本研究期間,承蒙曾文水庫管理中心洪燈河先生協助,以全球定位系統針對計算案例之雨量站進行座標位置校正,中央大學太空及遙測中心饒見有研究員提供 DTM 圖檔格式資料,仲琦科技總公司林開輝先生及高雄分公司彭美香小姐提供 ArcView 圖檔格式資料,僅致謝意。
參考文獻
註釋
為尊重智慧財產權,特將本文所提及之各項軟體、商標及所屬公司名稱列出,以示尊重。列出說明如下:
本研究成果所發展之數值計算模式可於網際網路上自由下載,網頁位置為:
http://feitsui.hyd.ncku.edu.tw/TLCheng/Thiessen/
| 站名 | X | Y |
| 曾文新村 | 197718.8630 | 2569022.3280 |
| 水山 | 230846.6873 | 2596842.7907 |
| 樂野 | 221906.0830 | 2595626.7100 |
| 里佳 | 220555.6620 | 2587293.0370 |
| 表湖 | 214445.8110 | 2573340.9600 |
| 馬頭山 | 208614.6510 | 2581784.6410 |
| 龍美 | 214655.9800 | 2589920.7080 |
| 三角南山 | 207017.4450 | 2569730.8090 |
| 大棟山 | 201190.6210 | 2578669.5970 |
| 站名 | 高度平衡加權因子 | 徐昇加權因子 | 圖 9
之高度 平衡加權因子 |
圖 9
之徐 昇加權因子 |
| 曾文新村 | 0.0122777 | 0.0054410 | - | - |
| 水山 | 0.1081453 | 0.0992032 | - | - |
| 樂野 | 0.1316063 | 0.1351530 | 0.4152013 | 0.2882259 |
| 里佳 | 0.1157133 | 0.1812786 | - | - |
| 表湖 | 0.1774671 | 0.1353215 | - | - |
| 馬頭山 | 0.1841478 | 0.1779597 | - | - |
| 龍美 | 0.1070878 | 0.1042925 | 0.1270550 | 0.3685434 |
| 三角南山 | 0.0730889 | 0.0808691 | - | - |
| 大棟山 | 0.0904657 | 0.0804811 | 0.4577438 | 0.3432307 |
圖 1 高度平衡多邊形法圖形結果展示
圖 2 高度平衡加權因子分析結果展示
圖 3 兩點高程平均中點接近三角南山
圖 4 超過 3 點以上兩點高程平均中點
圖 5 自相交之高度平衡多邊形
圖 6 匯入 ArcView 圖檔
圖 7 利用 ArcView 展示畫面
圖 8 徐昇多邊形法計算結果展示
圖 9 線性分布的雨量站所構成之控制面積分配