，在分析時亦受系統座標最小解析度限制。多邊形交集分析在徐昇加權因子計算之探討
| *鄭子璉 | **周乃昉 |
摘要
地理資訊系統經常運用交集、聯集、差集等分析以得到新的圖元，在進行複雜之幾何計算時，商用套裝軟體提供的功能往往不能完全滿足所需，必須另外購滿延伸套裝組件方能順利分析，例如在 ArcView 或 MicroStation 中，無法直接設定兩多個多邊形集合進行交集分析，必須單一逐次交互選取圖元交集，在 Arc 系統軟體處理多邊形的交、聯集分析時，以格網近似表示圖元邊界，不但使求得的多邊形圖元邊線座標點總數遽增，且連結後形成階梯狀，造成圖形失真，且可能引致運用上的困擾，在 MicroStation 中以長整數為格點，直接限制了座標點解析度及座標有效位數小於長整數有效位數。
本研究發展兩任意多邊形交集分析的計算方法，針對利用計算機分析幾何圖形所需考慮的數值處理及精度要求做檢討；再以徐昇多邊形網與集水區邊界的交集分析為應用例，可用電腦迅速求得各雨量站控制之多邊形區域的邊線點座標及面積，以正確求得徐昇加權因子，便於應用在區域平均降雨量的估算。
關鍵字：多邊形、交集、徐昇多邊形網法
Investigation of Intersection Analysis of Polygons in Estimating the Thiessen's Weighting Factors
Tze-Lien Tseng and Frederick N.F. Chou
Abstract
It is found that most of the Geographic Information Systems (GIS); package could not be able to meet the demand of the intersection analysis of complex geometry elements. Extended software packages are required in these cases. For examples, it is not possible to do the multi-polygon intersection analysis directly in the environment of ArcView and MicroStation. One should choose one by one between echo of the two polygons. Further more in Arc systems, mesh grids is implemented; much of data points in the intersection of polygon will be increased. The boundary of polygon will be rough like ladder. Some more problems will reveal later when we use the data of intersection of polygon. Moreover the format of all points has been restricted to long integer for private workspace unit.
In this study, a new algorithm for intersection analysis of any two polygons is developed. Investigation of the accuracy and related numerical methods are discussed. The algorithm is then applied to estimate the Thiessen's weighting factors. The validity of the algorithm is verified by analysis of the intersection of Thiessen's polygons and basin polygon. It has been proved that the performance of this algorithm shows good efficiency and accuracy. It could be applied to average rainfall estimation.
Key word: Polygon, intersection, and Thiessen's polygon method
一、研究背景與目的
在地理資訊系統幾何分析中常運用到圖元的交集、聯集、差集等分析，惟此類分析之計算方法均包裝於現成套裝軟體內，在進行複雜之應用分析時，若現成套裝軟體的功能不敷使用，則在處理較複雜問題時會造成應用上的困難，且分析結果可能會不適用於特定目的之研究。
例如，在 ArcView 3.x 及 Arc/INFO 7.x
的圖元分析功能中， Arc 在圖元之交集、聯集、差集等運算採用格網進行分析，故分析完成後求得的多邊形之總座標點數會遽增，且多邊形邊界的多重折線會以格網方式連結形成階梯狀，若經過多次的交集、聯集、差集等運算，圖元會因使用格網分析而使得多邊形的邊界座標點失真，分析完成後圖元資料在其後運用上會運算時間增加、儲存檔案空間增加及降低圖元解析度，造成圖元資料運用上的困擾。在
MicroStation
內，系統限制所有座標必須對映至長整數座標系統，座標最小解析度約為
，在分析時亦受系統座標最小解析度限制。
在地理資訊系統每個圖元交集、聯集、差集等分析中，兩任意圖元可能是線段、弧、扇形、圓及多邊形等的任意組合，而各種組合中以與非凸多邊形的圖元運算分析最為複雜，在非凸多邊形的交集、差集分析中，有可能因複雜的非凸多邊形而使得分析結果得到兩個以上的分離圖元，而在凸多邊形或線段、弧、扇形、圓等的交聯等分析較單純，分析結果一般均為單一圖元。
本研究先探討兩任意多邊形交集分析所需應用的方法，並針對幾何圖形應用於電子計算機上所需考量的數值問題及精度做探討；其後以徐昇多邊形網分析為應用研究實際分析所得成果，利用徐昇多邊形網與集水區邊界交集求得各徐昇多邊形的控制區域交集座標點及面積，可迅速求得徐昇加權因子，便於應用在面積平均降雨量的估算。
二、研究方法
在兩非凸多邊形進行交集分析時，先以兩多邊形相交的交點座標，將兩多邊形切成多段之多重折線，並逐一判斷兩多邊形所切成多段之多重折線所有座標點是否在另一多邊形內，分別剔除所有未在另一多邊形內的多重折線，所得之所有座標點即為欲求交集多邊形邊界座標，依序逐一串接交集多邊形邊界座標及交點座標，即可得完整之交集多邊形。因此，必須對多邊形中之一任意點是否在另一多邊形內的判斷原則進行研究。
在空間中之一任意點可位在多邊形內、在多邊形外及在多邊形上等三種情況，若在多邊形上又可細分成在線段上或在線段端點上。若將點與多邊形畫在同一圖紙上以肉眼判斷，可以很容易看出點與多邊形的關係，但在數學上要判斷如圖 1 所示之「任意點是否在多邊形內」，可考慮自該點做任一方向射線求取多邊形與射線的交點數，若為奇數則可得知點在多邊形內；若為偶數（包含 0 ）則可知點在多邊形外。但此種方法仍有例外情況存在，例如射線與多邊形相切於某一端點，或射線與多邊形之一邊恰巧重合，或該任意點恰巧落在多邊形上。
本研究則採用「多邊形各頂點依序對任意點求取角度差之總合」來判別任意點是否在多邊形內。計算如下式：
 |
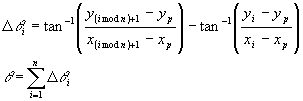(1) |
式中，
| n | = 多邊形總點數 |
 |
= 所需判斷之任意點之座標 |
 |
= 多邊形上第 i 點之座標 |
 |
=第 i 點與第 i+1 點角度差 |
在式 (1) 中，計算結果可能如式 (2) ，
 |
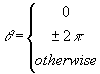(2) |
當 
計算結果為 0
時，任意點在多邊形外；當計算結果為 
時，任意點在多邊形內；當計算結果為其它值時，任意點在多邊形的端點上。其分析原理可藉由圖 1 來協助說明之。
在圖
1 中，當任意點在多邊形外，各邊頂點與任意點的角度差累加為
0 ，且角度差和變化量由 0 增加再減少，至最後一多邊形頂點與起點之角度差變化量恰巧合為
0 ，若任意點在多邊形內時，各邊頂點與任意點的角度差會沿著多邊形旋轉一圈，故累加為
；當任意點落在多邊形的端點上，由於同一點不能做夾角分析，因此最後計算結果會等於任意點前後兩邊的角度差值。
在這其中之特例為當任意點位在多邊形的線段上時，其角度差和為
0 ，但在其計算過程中必有一個角度差值為 
，因此當任意點在多邊形外時，又可細分為，當角度差
計算過程中出現為 時，任意點在多邊形的線段上；否則任意點在多邊形外。
在式 (2) 中，若計算結果為
時，可以另外獲得多邊形座標點排列順序旋轉方向之資訊，當計算結果為正值時，可以推得多邊形座標點排列順序沿正方向旋轉，即為沿逆時鐘方向旋轉；反之，當計算結果為負值時，可推得多邊形座標點排列順序沿負方向旋轉，即為順時鐘方向旋轉，可分析欲求交集多邊形座標點排列順序之關係，在進行依序逐一串接交集多邊形邊界座標及交點座標時，方不致發生交集多邊形座標連結錯亂。
多邊形面積之計算，如 (3) 式：
 |
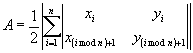(3) |
式中，
| n | = 多邊形總點數 |
| A | = 多邊形面積 |
|
= 多邊形上第 i 點之座標 |
三、分析步驟
本研究採用之兩任意多邊形的交集分析步驟如下：
在進行兩多邊形的交點分析時，兩線段的交點可採解兩直線方程式的二元一次聯立方程式進行計算，若兩直線平行時為無解，若兩直線恰可交於一點時為唯一解，若兩直線重合則為無限多組解；其狀況可運用高斯消去法演算完成的最後一式判定。但若為唯一解時，並不代表兩線段一定有交點，應增加判別交點是否落在兩線段上而非線段外。
欲檢查任意點是否落在線段上可使用兩種方式且都成立：
1. 空間幾何關係
任意點若在線段上，則任意點座標應在線段兩端點座標之間，任意點之點座標必不同時大於或小於兩端點座標，其表示式如下式：
 |
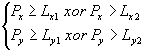(4) |
式中，
 |
= 所需判斷之任意點座標 |
 |
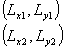= 線段兩端點之座標 |
2. 直線方程式
任意點若在線段上，則任意點座標應在線段所形成之直線方程式上，其表示式如下式：
 |
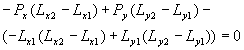(5) |
本文中兩線段的交點座標已採聯立解兩線段之直線方程式而得，所以交點座標必在兩線段上，因此僅需檢查交點座標與兩線段的空間幾何關係，若交點座標均在兩線段的端點座標內，則兩線段必有交點。
四、應用實例
集水區面積雨量的一般常用以估算方法有算數平均法、徐昇多邊形法、高度平衡多邊形法、等雨量線法等。除算數平均法不需經過交集分析外，其餘各分析方法均需先分析具有多個多邊形的集合後，再與集水區邊界多邊形交集求得各區域面積。本研究則應用上述交集分析技術在計算徐昇多邊形的加權因子上。
徐昇多邊形網法 (Thiessen Polygon Method) 是估計區域平均降雨量所最常用的方法，雨量站在空間的分佈位置並不均勻，徐昇多邊形網以經由決定各雨量站之影響控制面積方式，調整估計區域的平均降雨。一座雨量站在集水區內的影響控制面積對全區面積之比例，是為該測站的加權因子，可用以計算集水區的平均降雨量，而各雨量站所控制面積之範圍，概念上為該範圍內之任一點，至該雨量站之距離均較至任何一雨量站為近。在前述之分析中，可以將此加權因子之計算程序歸納如下：
1. 將相鄰之雨量站以直線相連，構成三角形網。
2. 依序連接各三角形之外心，或其邊之垂直平分線形成 N 個多邊形，即為徐昇多邊形網。
3. 將徐昇多邊形網與集水區邊界之多邊形交集，求出各雨量站在集水區內的控制面積
。
4. 各雨量站的徐昇加權因子，即為該雨量站的控制面積與集水區面積之比值：
 |
(6) |
式中，
 |
= 徐昇加權因子，無因次 |
| A | = 集水區面積 |
5. 集水區平均降雨量可以下式計算：
 |
(7) |
式中，
 |
= 各雨量站之降雨量； |
 |
= 集水區平均降雨量。 |
以此法求出之平均降雨量精確度較算術平均法為佳，亦是最常用的區域平均降雨量計算法。由於徐昇多邊形多以人工方式繪製，須耗費相當的時間及人力，其中若有一雨量站移動、增設或裁撤，則整個徐昇多邊形網便須重新繪製。
本研究採曾文水庫集水區為計算案例。曾文水庫集水區內外目前共有九個電傳雨量站，在防洪運轉過程中若發生電傳雨量站故障，便應立即依正常作業中之電傳雨量站重新分析徐昇加權因子，以推估平均降雨，若能應用電子計算機進行分析，將可大幅提高分析效率。
實例分析座標採用國際通用之橫麥卡脫投影二度分帶座標系統，以東經 121 度為中央投影線，曾文水庫集水區約在 (197000, 2567000) ~ (233000, 2603000) 之間，座標單位為公尺；為求精確計算各雨量站所控制之面積，在研究中利用全球定位系統 (GPS) 將各雨量站座標校正後加入分析。
五、結果與討論
5.1 分析結果
圖 2 為已分析完成的螢幕畫面，圖面展示了分析完成之三角網、徐昇多邊形網及與集水區邊界多邊形交集完成的控制區域，以 Pentium 233 MMX 計算此案例約共需 9 秒 (雨量站 9 站，邊界多邊形 688 點) ，三角網及徐昇多邊形網分析部分約佔 1 秒，徐昇多邊形網集合與流域多邊形集合交集約需 8 秒，同一案例若以 ArcView 3.1 配合額外購買空間分析模組 (Spatial Analyst 1.1) 的 Proximity 及交集分析約需 1 ~ 4 小時，依所設定分析之格網密度而定。
就模式計算之時效性來說，計算速度尚在能接受的範圍內，所運用的編譯器為 Visual Basic 5.0 中文專業版，分析模組可在一般慣用之 32 位元之視窗環境系統上執行 (Win32) 。
兩多邊形交集分析亦採用幾何方式分析，較 ArcView 3.x 以格網分析精確，分析後的多邊形點數僅增加交點座標，不似 ArcView 3.x 以格網分析會產生階梯狀之失真邊界，多邊形點數因階梯狀而暴增。
電子計算機因有效位數的限制，導致分析結果亦有些微之誤差，圖 3 為徐昇加權因子輸出表螢幕畫面，圖 3 表格中徐昇網交集面積欄之單位為平方公尺，在應用計算案例中，集水區面積換算後約為 482 平方公里，「其它」列為電子計算機在計算各雨量站控制面積累加之計算誤差，換算後約為 303 平方公分，在與集水區面積的比值上，這個誤差極小可以忽略不計。
5.2 研究討論
在研究進行中，發現利用電腦進行分析可大量縮減徐昇多邊形網製作的時間，但在利用電腦進行分析時，部分電子計算機的限制，在分析工具及技術上設限，需先行了解並研究相關問題之癥結，避免實際研發時發生不可預期的失敗。
1. 危險圓
在計算處理三角網時，若遇上四個以上的雨量站點共圓之「危險圓」情況，兩個以上的三角形有可能會重疊，產生分析徐昇多邊形網的錯誤，發生機會很小，即使是數學上的共圓情形，也有可能因計算機誤差造成不共圓。
處理方式可以任意頂點為端點，依序連結非相鄰的頂點形成三角網，在徐昇多邊形網的分析部分可知會由各相鄰頂點中點連往危險圓圓心，因此可知只需三角網不發生重疊，則危險圓上的三角網不論如何形成，必定不會影響徐昇多邊形網的分析。
2. 分析範圍邊界
靠近圖面邊緣的雨量站之徐昇多邊形多無法閉合，而外心中垂線將無限延長至無窮遠，因此不但不能計算徐昇多邊形面積，也無法執行交集分析。為解決此種情況，本研究根據以有限圖紙分析徐昇多邊形網之方式，由雨量站位置座標點與集水區邊界之資料點中找出最小及最大的 x 值與 y 值，並向圖面外延伸各軸邊長的 5% 做為分析範圍邊界的頂點，憑以繪一矩形視為圖紙邊緣並當做分析範圍邊界。再針對各徐昇多邊形逐一檢查其是否閉合，非閉合的徐昇多邊形則由中斷處向外延伸至分析範圍邊界，依正方向（逆時針方向）繪成一閉合多邊形；若原為閉合的徐昇多邊形則與分析範圍邊界進行交集分析，以交集完成之徐昇多邊形取代超過分析範圍邊界的徐昇多邊形。附帶的，加入分析範圍邊界亦可使輸出之圖形較美觀，可依圖面內容完全展示在螢幕或圖紙上。
3. 座標點解析度與電子計算機有效位數
在 Visual BASIC 中，預設變數是 Variant 型態，其變數精確度在實數方面可比照倍精度變數，因此可知至少具有 15 位以上的精確度，而在判斷二線段是否重合、相切，或點是否相同時，有時會因受到計算機變數的誤差限制，在數學上或實際上是同一點的情況中，有可能在計算機中會有極小不同的誤差，例如將點座標代入直線方程式時，可能因為點座標或直線方程式之係數為無理數，而無法以有限位數表達，因此本研究中選用相對誤差做判斷標準，並取 10-10 為容許誤差的門檻值，藉此判別是否為同一點或某點是否在目標直線方程式上。
台灣地區二度分帶座標值位數過大但實際座標變動量小，分析計算案例曾文水庫集水區座標範圍約在 (197000, 2567000) ~ (233000, 2603000) 之間，以 y 方向之座標軸來說，小數點以上即有 7 位數，若採用容許誤差為絕對精度 10-10 ，則容許誤差應用於本研究案例，會比計算機可使用 15 位有效位數還小 2 個值級，形成容許誤差完全失效，因此必須改採用容許誤差為相對精度 10-10 ，並於計算分析時改採相對座標，將座標值未變動之值級部分進行座標平移，使分析計算案例曾文水庫集水區座標範圍變更為 (197000, 567000) ~ (233000, 603000) 之間，即為將 y 方向之座標值減去 2000000 ，僅於實際對外部進行輸入輸出時才採用絕對座標，提高電子計算機有效位數的運用。
在檢查任意點是否在線段上所使用兩種方式均有容許精度的問題，在空間幾何關係分析上，判別兩點是否為同一點時，可能因有效位數的影響，造成同一點可能座標值略有不同，這對串接多重折線成一多邊形時可能造成困擾，在代入直線方程式分析上，可能無法很精準的恰巧等於 0 ，因此配合採用容許誤差為相對精度 10-10 ，使得電子計算機因有效位數對計算所造成的誤差能消除。
以高斯消去法解得之兩線段交點會因兩直線方程式的求取過程而有可能稍有差異，如直線方程式在計算常係數時代入不同的線段端點座標，則有可能發生常係數在有效位數最後 1 ~ 2 位數不完全相同的情況，又兩直線方程式在求解的係數矩陣順序上的不同，亦有可能解出在有效位數最後 1 ~ 3 位數略有差異的交點座標，在高斯消去法分析之前可先對輸入之係數矩陣依序排列，以使同一組直線方程式組必解出相同交點座標，另需對所產生之直線方程式係數約分，如此可使兩直線方程式之係數在同一值級上，可避免在消除係數的步驟時，誤差位數過度放大而影響正確的計算。
4. 聯集與差集分析
在交集分析步驟中，「檢查各段多重折線是否在另一多邊形內，若不在另一多邊形內則捨去本段多重折線。」在此步驟中改以「檢查各段多重折線是否『不在』另一多邊形內，若『在』另一多邊形內則捨去本段多重折線。」則可將交集分析輕易的修改成聯集分析步驟，同理可修改此步驟之邏輯判斷將交集分析步驟變更為差集分析步驟。
5. 與現成套裝軟體交集分析比較
圖 4 為套裝軟體 ArcView 軟體交集分析後的部分邊界放大展示，在 ArcView 的交集分析功能中，會在交集邊界上形成階梯狀，在圖中可以很清楚的展現格網方式分析對多邊形的邊界點數增加的影響，在運用 ArcView 進行圖元分析原數化座標點為 558 點之多邊形，經過數次交、聯、差集分析，多邊形已迅速增為 2,203 點，又在 ArcView 中需設定座標解析度，此一設定亦限制其在交集分析上的交點座標必位於格點上，雖然其座標可以以倍精度儲存，但仍無法將比格網還精確的座標顯示在圖面上，計算求得之交點座標必須經過適當的進位至格網座標精度方能順利於螢幕上展示，在本研究所發展的計算模組僅增加交點座標，其餘座標均為原多邊形數化座標，交點座標完全使用倍精度可用的最多位數表示，在分析及應用上座標值失真較小。
6. 多邊形處理注意事項
多邊形在幾何分析上是連續且循環的圖形，並沒有起始點或終點，但在紀錄時會以某一頂點為起始點，因此分析時應特別注意終點座標與起始點座標之間的連續性。
六、結論與建議
6.1 結論
6.2 建議
謝誌
在本研究期間，承蒙曾文水庫管理中心洪燈河先生與林淑真學姊協助，以全球定位系統針對計算案例之雨量站進行座標位置校正，邊孝倫學妹協助計算案例的座標數化及整理，並協助測試計算分析模式，僅致謝意。
參考文獻
註釋
為尊重智慧財產權，特將本文所提及之各項軟體、商標及所屬公司名稱列出，以示尊重。列出說明如下：
本研究成果所發展之「徐昇網自動分析」模式可於網際網路上自由下載，網頁位置為：
http://feitsui.hyd.ncku.edu.tw/TLCheng/Thiessen/
圖 1 任意點與多邊形的關係
圖 2 計算案例三角網、徐昇多邊形網分析完成圖
圖 3 計算案例徐昇加權因子分析結果展示
圖 4 ArcView 交集完成部分邊界放大展示圖