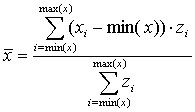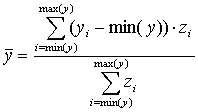GEOMETRY ALGORITHM OF HEIGHT BALANCE POLYGONS METHOD FOR ESTIMATING THE AREAL RAINFALL OF WATERSHED

Tze-Lien Tseng , and Frederick N. Chou

Department of Hydraulics & Ocean Engineering, National Cheng Kung University, Tainan 70148, Taiwan

devil@mail.hyd.ncku.edu.tw, hyd4691@mail.ncku.edu.tw

¡@

Abstract

¡@¡@ In Taiwan, the most frequently adopted algorithms in estimating average rainfall within a certain watershed are Arithmetical Averaging Method, Thiessen Polygons Method, and Isohyeatal Method. Because of involvement of geographic elevation factors in the estimation, when evaluating the average rainfall in rugged and craggy area, Height Balance Polygons Method (HBPM) is more accurate than the former three estimation algorithms. However, complicated calculation and analysis procedures make itself less applicable in the routines of estimating average rainfall.

¡@¡@In order to estimate real-time average rainfall in the field, a computerized HBPM model was developed. This numerical module quickly processes the triangulated irregular networks (TIN), center of elevation of TIN, height balance polygons and height balance weight factors with DTM data and ArcView format. Besides, two suggestions were post in this study; (1) using weight central point instead of central point of elevation in the computation process and, (2) applying the angular bisector at the auto-intersection of the height balance polygons.

Key words: height balance polygons, triangulated irregular networks, areal rainfall, watershed

¡@

1. Introduction

¡@¡@Arithmetical Averaging Method, Thiessen Polygons Method (TPM), and Isohyetal Method are widely adopted for estimating the areal rainfall of watershed in Taiwan. However, these three estimations are less practical and accurate when rugged and craggy topography is taken into account, often, the Height Balance Polygons Method (HBPM) is superior to the former estimation methods. The main difference between HBPM and the other is that weighted functions are calculated according to the elevations of rainfall gauges; namely, topographic factors are involved in the estimation. However, due to the complexity of calculation, the HBPM is difficult in routine operation.

¡@

2. Literature review

¡@¡@Implement of 2D graphic analysis can be through two ways, which are Computing Geometry and Computing Graphic, i.e. vector analysis and grid analysis. When applying HBPM in digital programs, it is difficult to calculate center of elevation of Triangulated Irregular Networks (TIN) by grid analysis. Therefore, vector analysis is a way to implement HBPM in computerized programs.

¡@¡@The approach steps before vector analysis of TIN of HBPM, there are no differences between HBPM and TPM. In TPM studies, most researchers adopted grid analysis as the step of TPM, because the approach steps have to fit 2D graphics software, like Proximity of Spatial Analyst of ArcView, which involves grid analysis technique. Only few researchers studied TPM with vector analysis. (F. N. Chou and T. L. Tseng, 1995~[1-3]) Another drawback of grid analysis is suitable for simple computation. High numerical resolutions need more computing time. Although there are advantages in graphic and computation of vector analysis, HBPM is still not popular because of its complex estimation steps. That's why concept of HBPM had been post at textbook in 1970 [4], but after a long time, two rules for improvements of HBPM have been present by few writers (T. L. Tseng et al. [5]) until 1999.

¡@

3. Methods

¡@¡@Steps of HBPM are as follows

  1. Digitize rain-stations and watershed polygon information,

  2. Triangulate irregular networks,

  3. Estimate central points of elevation between two rain-stations,

  4. Connect all elevation of central points of TIN,

  5. Create height balance polygons,

  6. Analyze intersection polygons between height balance polygons and watershed polygon and,

  7. Compute elevation weights of HBPM.

¡@¡@TIN of HBPM is same as TIN of TPM, which means there is no rain-station inner circumcircle of any three rain-stations. The following will introduce the calculation of each step.

3.1 Center of elevation of TIN

¡@¡@Central point of elevation between two rain-stations can be estimated by midpoint of weighted elevation of profile. Formula is as follows,

¡@

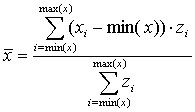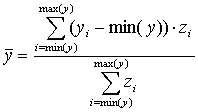, (1)

¡@¡@Where

  = Coordinate of midpoint of center of elevation
= Interpolation coordinate of elevation of profile between two rain-stations

¡@¡@Model can automatically search all of sub-directories to find needed data files of DEM. To reduce numerical errors, coordinates of points are interpolated on grid (Fig. 1). Connection of all points of center of elevation can be formed TIN.

3.2 Height balance polygons

¡@¡@Extending lines from incentre of incircle to apexes of center of elevation of TIN to boundary of computing and connecting all polylines will make closed polygon. Boundary for computation is like edge of paper, which will make all polygons having limit computing domains, which also let view window of all graphics on screen and paper.

3.3 Intersection

¡@¡@Weight factors within a polygon of HBPM have to be confined in watershed, therefore intersection between height balance polygons and watershed polygon needs to analyze. Steps in analysis of intersection polygons (Fig. 2):

  1. Let polygons rotates along anti-clockwise direction,

  2. Find all points of intersection between two polygons,

  3. Separate polygons to multi-polylines from intersect points,

  4. Keep polylines inside another polygon,

  5. Connect every polylines from any polyline along intersect point, and

  6. Repeat step 5 until all polylines become closed polygons.

3.4 Weight of HBPM

¡@¡@Calculation of weight of HBPM is the same method as that of TPM is estimated. The weight can be provided for calculating average rainfall in watershed. Computing weights of HBPM is

¡@

(2)

¡@¡@Where

= Weight of HBPM
= Every area of intersection polygons
A = Area of watershed

fig.1¡@ get points of EL. on profile of vertical section

fig.2¡@intersection of two any polygons

¡@

4. Results

¡@¡@In this study, estimation of the areal rainfall within Tsengwen reservoir watershed is as an example (Fig. 3). With the presented geometry algorithm, performance is good in less CPU time. When using CPU of Pentium 233 MMX on calculating the watershed with 9 rain stations and 688 points of boundary polygon, it takes approximately 10 s. The relative errors of accumulate of HBPM is less then 10-14. It is rather efficient to compare manual work, which needs 3 to 7 workdays.

¡@¡@The HBPM geometry algorithm has been developed by Microsoft Visual Basic, which supports the DEM data, ArcView format and enhanced metafile (EMF) for Win32 operating systems. This algorithm calculates the triangulated irregular networks (TIN), center of elevation of TIN, height balance polygons, and height balance weight factors respectively in less CPU time. This study provided an algorithm for the weight computation of intersection analysis of any two polygons, which improves the computation efficiency, and lets the real-time average rainfall estimation in the operational monitoring system become feasible.

(a) Graphic of HBPM

(b) Table of HBPM

fig.3¡@Graphic of HBPM on Win32 by screen copy

¡@

5. Discussions

5.1 Point of center of elevation

¡@¡@In literature review, central point of elevation is the same as midpoint of average elevation. In Tsengwen reservoir watershed, non-uniform distributive rain-stations let weight of HBPM is being unreasonable. For example (Fig. 4(a)), in the profile of two rain-stations between SanJiauNanShan and BeouHwu, the midpoint is too close SanJiauNanShan. In this condition, weight of HBPM will be too small to calculate areal rainfall. In another example (Fig. 4(b)), in the profile of two rain-stations between DaDungShan and LaYa, 11 points can be provided to treat as the midpoint. There is no criterion for selecting the best one of them. Therefore, this study suggested that midpoint of weight of elevation of profile replace midpoint of average elevation.

5.2 Import and export ArcView shape file

¡@¡@There have been existed some software of GIS that have digitized functions; therefore, this model didn't include this module. 2 files format of ASCII and ArcView shape file can be input into this model [6] (Fig. 5(a)) and 3 files format, ASCII, ArcView shape file (Fig. 5(b)) and Enhanced Metafile (EMF) can be output of this model. Sometimes when ArcView processed intersection of two polygons, intersection polygon maybe became like a ladder. However in this model, after intersection analysis, the geometry algorithm only insert points of intersection, which can keep polygon initiative digitizes exact. The polygon does not become stairs boundary after multi-intersection.

(a) Import

(b) Export

fig.5¡@ArcView shape file of HBPM by screen copy

5.3 Modify HBPM

¡@¡@Extending line form incentre of incircle to apexes of center of elevation of TIN till boundary of computing maybe cause the intersection point of the extending line (Fig. 6(a)). Overlap polygons cause double calculation. In this study, when overlap occurred, a diagonal line is used from intersection point until boundary to modify the polygons of HBPM (Fig. 6(b)).

5.4 Compare with TPM

¡@¡@In TPM, only 2D distributive rain-stations are taken into account (Fig. 7), which is also a popular criterion for estimation of areal rainfall. Comparison of all rain-stations, weight of HBPM is similar to TPM (Table 1). In case 1 and case 2 (Fig. 8), almost parallel distributive rain-stations have been selected. At ends, weight of HBPM is larger than that of TPM. In case 3 and case 4, locations of distributive rain-stations are like "U". The analysis results also show that at two end points weight is larger in HBPM than in TPM. In the examples, weight of HBPM may be unreasonable, TPM maybe a better strategy HBPM.

Get File of EMF

Fig.7¡@ Export to EMF of TPM

Table 1¡@Comparing Weight of TPM and HBPM

Station Name TsengWen ShuiShan LaYa LiJia BeouHwu MoaTou-Shan LungMei SanJiau-NanShan DaDung-Shan
Weight
 of
TPM		 All 0.0054 0.0992 0.1352 0.1813 0.1353 0.178 0.1043 0.0809 0.0805
a-1 0.0726 - 0.2882 - - 0.4167 0.2224 - -
a-2 0.0726 - 0.405 - - 0.5223 - - -
a-3 0.024 0.3607 - - 0.4463 - - 0.1691 -
a-4 0.0359 0.1004 0.3046 - - 0.4468 - - 0.1123
Weight
 of
HBPM		 All 0.0123 0.1081 0.1316 0.1157 0.1775 0.1841 0.1071 0.0731 0.0905
b-1 0.4636 - 0.391 - - 0.0222 0.1232 - -
b-2 0.3788 - 0.3798 - - 0.2413 - - -
b-3 0.5232 0.2717 - - 0.1817 - - 0.0234 -
b-4 0.4284 0.149 0.1824 - - 0.1512 - - 0.0891

¡@

6. Conclusions

¡@¡@Based on the previous discussions, some suggestions are as follows:

  1. In the computation processes, the central point of elevation should be replaced by weight central point.

  2. Apply the diagonal line at the intersection point when the height balance polygons overlap occurred.

  3. When distributive rain-stations are like "U" or line, weight of HBPM may be unreasonable.

  4. Inputting digitized data and proceeding all of analysis in this model need 15 minutes, total of work times are fast than work done by hand.

  5. The numerical errors are less than 10-14 that can be ignored. Intersection points that can keep original digitized resolution only have inserted intersection polygon.

  6. You can find the model of this study at http://feitsui.hyd.ncku.edu.tw/TLCheng/Thiessen/.

¡@

References

  1. F. N. Chou and T. L. Tseng, "Thiessen Method in Auto-Computing", 1995 Proceedings of the Conference on Computer Applications in Civil & Hydraulic Engineering, Taiwan, pp. 465 - 476, Oct. 1995.

  2. T. L. Tseng and F. N. Chou, "Investigation of Intersection Analysis of Polygons in Estimating the Thiessen's Weighting Factors", Proceedings of the 10th Hydraulic Engineering Conference, Taiwan, pp. I39 - I46, Jul. 1999.

  3. T. L. Tseng¡BF. N. Chou, "Numerical Algorithm of Thiessen Polygons Method", Journal of Taiwan Water Conservancy, 48(3), Taiwan, pp. 43 - 51, Sep. 2000.

  4. S. D. Xu, S.R. Zhu and W.Q. Lei, "Applied Hydrology", DongHua, Taiwan, pp. 247 - 250, Feb. 1976.

  5. T. L. Tseng, F. N. Chou and W. H. Hu, "Numerical Algorithm of Height Balance Polygons Method", 1999 Proceedings of the Conference on Chinese Geographic Information Society, Taiwan, pp. 2, Dec. 1999.

  6. ESRI, "ESRI Shapefile Technical Description - An ESRI White Paper", Jul. 1998.